3.7 softmax 回归简洁实现

要点（基本步骤）

nn.init.normal_(m.weight, std=0.01)：初始化参数，这里的 m 是 Sequential 里的模块
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) ：定义网络，一层展平，一层全连接
loss = nn.CrossEntropyLoss(reduction='none')：交叉熵损失
trainer = torch.optim.SGD(net.parameters(), lr=0.1)：SGD 优化器
计算损失

1. 初始化模型

导入数据集，保持批的大小为 256

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

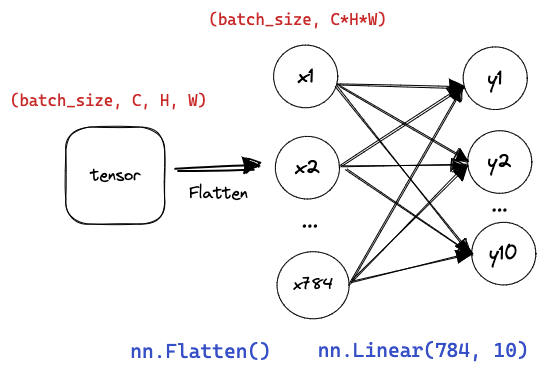
PyTorch 不会隐式地调整输入的形状，必须先展平。定义网络结构：
该网络有两层，第一次为展平层，注意 Pytorch 中始终第一维为样本个数

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01) # 下划线结尾的函数都表示原地更新

net.apply(init_weights);

Sequential 定义的对象可以理解为一些模块的容器，apply() 方法对里面的网络层循环调用init_weights方法

2. 重新审视 Softmax 的实现

回忆 sofmax 函数 :

$\hat{y} = softmax (o) 其中 {\hat{y}}_{j} = \frac{\exp (o_{j})}{\sum_{k} \exp (o_{k})}$

在数学上这套理论没有问题，但数值上碰到指数额外要注意，如果中的一些数值 $o_{k}$ 非常大，那么 $\exp (o_{k})$ 可能大于数据类型容许的最大数字，即_上溢_（overflow）。这将使分母或分子变为 inf（无穷大），最后得到的是0、inf 或 nan（不是数字）的 $\hat{y}$ 。在这些情况下，我们无法得到一个明确定义的交叉熵值。

对于无穷除以无穷的处理，一个技巧就是同时放缩，都除以一个 $\exp (max (o_{k}))$

\begin{array}{r} \begin{aligned} {\hat{y}}_{j} & = \frac{\exp (o_{j} - max (o_{k})) \exp (max (o_{k}))}{\sum_{k} \exp (o_{k} - max (o_{k})) \exp (max (o_{k}))} \\ = \frac{\exp (o_{j} - max (o_{k}))}{\sum_{k} \exp (o_{k} - max (o_{k}))} . \end{aligned} \end{array}

这样做避免了 $\exp$ 计算太大的问题，但交叉熵最后算的是 $\log$ ，上面分子可能有 0，尽管我们要计算指数函数，但我们最终在计算交叉熵损失时会取它们的对数。通过将 softmax 和交叉熵结合在一起，可以避免反向传播过程中可能会困扰我们的数值稳定性问题：

\begin{array}{r} \begin{aligned} \log ({\hat{y}}_{j}) & = \log (\frac{\exp (o_{j} - max (o_{k}))}{\sum_{k} \exp (o_{k} - max (o_{k}))}) \\ = \log (\exp (o_{j} - max (o_{k}))) - \log (\sum_{k} \exp (o_{k} - max (o_{k}))) \\ = o_{j} - max (o_{k}) - \log (\sum_{k} \exp (o_{k} - max (o_{k}))) . \end{aligned} \end{array}

注意

机器学习很多理论上没有问题，但实际实现上会有一些数值问题，例如：

碰到 $\exp$ 就要考虑上溢问题
碰到 $\log$ 就要考虑下溢问题
可以利用两者互相抵消

交叉熵损失：信息熵（information entropy）#^62c057

loss = nn.CrossEntropyLoss(reduction='none')

注意

这里 CrossEntropyLoss 已经对输入做了 softmax 运算，所以直接输入神经网络神经元的结果，不需要手动将输出的 y 转化为概率

3. 优化算法

使用学习率为0.1的小批量随机梯度下降作为优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

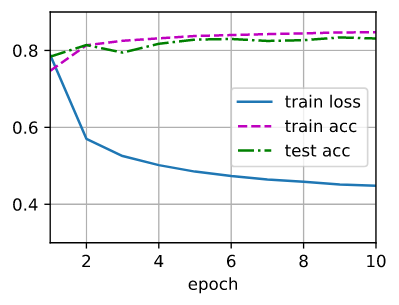
4. 训练

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

d2l.train_ch3 参考:

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad() # torch 的 SGD 学习器不会除以 batch_size
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0]) # 课程内置的 SGD 会除以 batch_size
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

算法使结果收敛到一个相当高的精度